
#MOMENT OF INERTIA EQUATION I BEAM FULL#
Other Parameters – These are more advanced results calculated by the full Sk圜iv Section Builder:
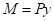
Torsion Constant (J) – also known as the polar moment of inertia or J, is a value that describes a material's resistance to twisting or torsional deformation.For instance, Szt is the section modulus about the Z axis to the top fibre of the section. They are usually calculated to the top and bottom fibres section. Zz, Zy in Britain or Australia) – Also known as statical section modulus, and are used in bending stress calculations. Elastic Section Modulus (Sz, Sy in America.The calculator will provide this value, but click here to learn more about calculating the first moment of area. These are typically used in shear stress calculations, so the larger this value the stronger the section is against shearing. Like the Moment of Inertia, these are in both the Z and Y direction.
#MOMENT OF INERTIA EQUATION I BEAM HOW TO#
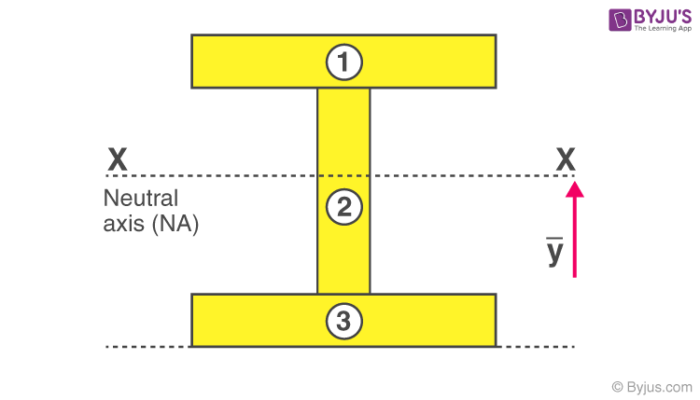
Learn how to calculate the centroid of a beam section. For non-symmetrical shapes (such as angle, Channel) these will be in different locations. For symmetrical shapes, this will be geometric center. Centroid (Cz, Cy) – this is the center of mass for the section and usually has a Z and Y component.See Moment of Ineria of a circle to learn more. Also worth noting that if a shape has the same dimensions in both directions (square, circular etc.) these values will be the same in both directions.This is because sections aren’t designed to take as much force about this axis Minor Axis (Iy) – This is about the Y axis and is considered the minor or weak axis.Major Axis (Iz) – This is about the Z axis and is typically considered the major axis since it is usually the strongest direction of the member.The higher this number, the stronger the section. Moment of Inertia (Iz, Iy) – also known as second moment of area, is a calculation used to determine the strength of a member and it’s resistance against deflection.Area of Section (A) – Section area is a fairly simple calculation, but directly used in axial stress calculations (the more cross section area, the more axial strength).Here is a concise list of the section property terms and definitions: 3 provides the moment of inertia and section modulus formula for common geometrical shapes.The moment of inertia calculator will accurately calculate a number of important section properties used in structural engineering. In SI unit systems the unit of Section Modulus is m 3 and in the US unit system inches 3. Section modulus is denoted by “Z” and mathematically expressed as Z=I/y The section modulus of a section is defined as the ratio of the moment of inertia (I) to the distance (y) of extreme fiber from the neutral axis in that section. The larger the moment of inertia, the greater is the moment of resistance against bending. Bending stresses are inversely proportional to the Moment of Inertia. A moment of inertia is required to calculate the Section Modulus of any cross-section which is further required for calculating the bending stress of a beam.

The Critical Axial load, Pcr is given as P cr= π 2EI/L 2. The moment of inertia “I” is a very important term in the calculation of Critical load in Euler’s buckling equation.A polar moment of inertia is required in the calculation of shear stresses subject to twisting or torque.Area moment of inertia is the property of a geometrical shape that helps in the calculation of stresses, bending, and deflection in beams.Mass moment of inertia provides a measure of an object’s resistance to change in the rotation direction.


 0 kommentar(er)
0 kommentar(er)
